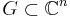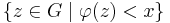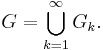Pseudoconvexity
In mathematics, more precisely in the theory of functions of several complex variables, a pseudoconvex set is a special type of open set in the n-dimensional complex space Cn. Pseudoconvex sets are important, as they allow for classification of domains of holomorphy.
Let
be a domain, that is, an open connected subset. One says that  is pseudoconvex (or Hartogs pseudoconvex) if there exists a continuous plurisubharmonic function
is pseudoconvex (or Hartogs pseudoconvex) if there exists a continuous plurisubharmonic function  on
on  such that the set
such that the set
is a relatively compact subset of  for all real numbers
for all real numbers 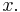 In other words, a domain is pseudoconvex if
In other words, a domain is pseudoconvex if  has a continuous plurisubharmonic exhaustion function. Every (geometrically) convex set is pseudoconvex.
has a continuous plurisubharmonic exhaustion function. Every (geometrically) convex set is pseudoconvex.
When  has a
has a 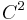 (twice continuously differentiable) boundary, this notion is the same as Levi pseudoconvexity, which is easier to work with. More specifically, with a
(twice continuously differentiable) boundary, this notion is the same as Levi pseudoconvexity, which is easier to work with. More specifically, with a 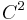 boundary, it can be shown that
boundary, it can be shown that  has a defining function; ie., that there exists
has a defining function; ie., that there exists 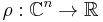 which is
which is 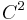 so that
so that 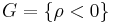 , and
, and 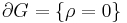 . Now,
. Now,  is pseudoconvex iff for every
is pseudoconvex iff for every 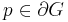 and
and  in the complex tangent space at p that is,
in the complex tangent space at p that is,
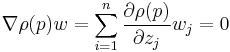 we have
we have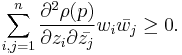
If  does not have a
does not have a 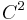 boundary, the following approximation result can come in useful.
boundary, the following approximation result can come in useful.
Proposition 1 If  is pseudoconvex, then there exist bounded, strongly Levi pseudoconvex domains
is pseudoconvex, then there exist bounded, strongly Levi pseudoconvex domains 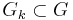 with
with 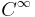 (smooth) boundary which are relatively compact in
(smooth) boundary which are relatively compact in  , such that
, such that
This is because once we have a  as in the definition we can actually find a C∞ exhaustion function.
as in the definition we can actually find a C∞ exhaustion function.
The case n = 1
In one complex dimension, every open domain is pseudoconvex. The concept of pseudoconvexity is thus more useful in dimensions higher than 1.
See also
References
- Lars Hörmander, An Introduction to Complex Analysis in Several Variables, North-Holland, 1990. (ISBN 0-444-88446-7).
- Steven G. Krantz. Function Theory of Several Complex Variables, AMS Chelsea Publishing, Providence, Rhode Island, 1992.
This article incorporates material from Pseudoconvex on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.